7. 메모리 관리 기법(3) - 페이징, 세그멘테이션

지금까지 메모리공간을 효율적으로 할당해보기 위해 연속메모리할당, 스와핑에 대해 알아보았다. 이로인해 발생하는 외부 단편화문제를 해결하기 위한 접근방법으로써 페이징이라는 메모리 관리 기법에 대해 알아본다.

페이징 (Paging)

페이지 (page) 단위의 논리- 물리 주소 관리 기법

논리 주소 공간이 하나의 연속적인 물리 메모리 공간에 들어가야 하는 제약 해결 

스와핑을 하는 경우에도 디스크에 연속적으로 저장될 필요 없음

 

페이징은 프로세스가 사용하는 메모리 공간을 잘게 나누어서 비연속적으로 실제 메모리에 할당하는 메모리 관리 기법이다. 그리고 이 잘게 나눈 것의 단위가 페이지라는 것이기 때문에 페이지라는 용어를 쓴다. 그리고 페이징 방식으로 메모리를 할당하게 되면 실제 프로세스가 실행될 때는 각각의 페이지들이 실제 메모리의 어디에 위치하고 있는지를 빠르게 알 수 있어야한다. 또 프로세스의 입장으로 보면 자신이 사용하고 있는 메모리 공간이 흩어져 있는 페이지들로 구성되는 것이 아니라 하나의 연속된 메모리공간으로 이해할 수 있어야지 프로그램 실행이 효율적이게 된다. 즉 프로세스가 바라보는 메모리의 주소 공간과 실제 메모리의 주소 공간을 논리 주소와 물리 주소라는 것으로 구분을 하고 그들 사이의 변환을 통해서 메모리 참조를 효율적으로 하고자 하는 참조 기법까지도 포함하고 있다. 이와같이 페이징은 효율적인 메모리 할당과 프로세스의 효율적인 메모리 참조라는 두 가지의 메모리 관리의 다 달성하고 있기 때문에 실제 대부분의 운영체제에서 관리하는 기본적인 메모리 관리 기법이라고 할 수 있다. 

필요조건

논리 주소 공간과 물리 주소 공간의 분리 - 주소의 동적 재배치 허용

전용 하드웨어 (MMU) - 논리 주소와 물리 주소의 변환

 

컴퓨터 시스템에 메모리 주소라는 개념을 프로세스의 논리 주소를 한 것과 실제 메모리의 물리 주소로 분리하여 동적으로 논리주소가 물리주소에 재배치되면서 할당되는 것을 허용해야 하고 또 모든 메모리 참조에서 주소변환이 필요하기 때문에 이것을 소프트웨어가 아닌 변환을 전용으로 해주는 MMU가 필요하게 된다.

 

 

프레임 (Frame) & 페이지 (Page)

프로세스가 바라보고 있는 메모리 공간 즉 논리 주소 공간이라는 것은 일정한 크기의 페이지들로 나누어지게 되고 각각의 페이지들은 실제 메모리의 연속된 위치가 아닌 각각의 페이지 별로 임의의 위치에 저장되고 할당 될 수 있다. 그리고 페이지가 저장된 메모리의 위치 영역을 프레임이라고 한다. 그래서 실제 프레임의 크기와 페이지의 크기는 일치한다. 프로세스의 메모리 공간을 얘기할 때는 그 단위를 페이지라고 얘기하고 실제 메모리에서는 프레임이라고 얘기한다. 그리고 일반적인 운영체제에서 페이지와 프레임의 크기는 보통 4KB가 된다. 그리고 이러한 할당에서 아주 중요한 역할을 하는 것이 page table이다. 단편 문제는 해결했지만 프로세스가 실행 될 때 자기는 연속된 위치의 메모리라고 이해한 상태로 각각의 페이지가 어디에 있는지를 매번 빠르게 찾을 수 있어야지만이 이 프로세스는 실행이 된다. 그래서 각각의 페이지가 실제 메모리에 어떤 프레임이 저장이 되는가에 대한 매핑 정보를 담고 있는 페이지 테이블이란 것이 바로 페이징을 운영하는 데에 있어서 매우 중요한 자료 구조이다. 페이지 테이블은 프레임 번호를 담고있는 배열이고 그것의 인덱스는 페이지 번호를 가리키고 있다고 할 수 있다. 그래서 페이지 번호를 가지고서 인덱스로 직접적으로 접근하게 되면 해당 페이지가 담고있는 프레임을 바로 알 수 있게된다.

 

페이징 (paging)의 주소 표현

페이징 기법에 따라 메모리를 운용하면서 우리가 알고 있는 주소를 조금 다른 관점으로 바라보게 된다. 이전의 주소값이라는 것은 한 바이트의 위치를 나타내는 주소값이였다. 하지만 페이징 기법에서는 실제 어떤 변수(논리 주소)가 저장되어 있는 어떤 바이트 주소(물리 주소)를 알아야 되긴 하지만 이것들이 페이지 단위의 묶음으로 배치가 되기 때문에 먼저 페이지가 어디에 있는지를 알아내야 한다. 다음에 그 안에서의 변수의 실제 바이트 위치는 페이지 안에서의 위치와 이 프레임 안에서의 위치가 일치하게 된다. 그래서 페이지가 어디에 있는가를 알아내는 것이 더 중요하다.

 

논리 주소 공간의 크기가 2^m이고, 페이지의 크기가 2^n일 때 상위 (m-n) 비트는 페이지 번호, 하위 n 비트는 오프셋이다.

논리 주소 구조

페이지 크기가 4KB이고 메모리 크기가 256KB인 메모리 페이징 시스템이 있다.

페이지 크기가 4KB라 하였다. 메모리 관련 개념에서는 사용되는 단위가 바이트(Byte)이므로 바이트로 우선 변환해보자.

그럼 페이지는 2^12 Byte임을 알 수 있다. 마찬가지로 메모리를 보면 메모리는 2^18 Byte가 됨을 알 수 있다.

 

- 페이지 프레임 수는? (페이지 번호 수 (상위 m-n비트) )

페이지 프레임 수는 메모리 전체 크기에 페이지가 최대 몇개 들어 갈 수 있는지 묻고 있는것이다.

따라서 2^18/2^12 = 2^6 = 64개이다.

 

- 이 메모리 주소를 해결하는 데 필요한 비트 수는?

메모리 주소를 모두 표현하기 위해서는 메모리가 2^18임을 알고있고 결국 비트가 18개가 있어야 2^18을 만족 할 수 있게 된다. 따라서 18비트가 있으면 된다.

- 페이지 번호에 사용하는 비트와 페이지 오프셋에 사용하는 비트는?

페이지는 모두 64개가 있다 했다. 따라서 그림은 다음과 같아진다.

페이징을 적용한 프로세스의 논리 주소

위의 그림에서 보면 알 수 있듯이 페이지 번호를 모두 나타내기 위해서는 6개의 비트가 있어야 

페이지 번호 0번(000000)부터 페이지 번호 63번(111111)까지 모두 나타 낼 수 있다.

그리고 오프셋에 사용되는 비트 수는 한 페이지의 모든 위치를 다 나타내기 위해 

k번 페이지의 0번(0000 0000 0000)부터 2^12-1번(1111 1111 1111)까지 나타내는 총 12비트가 필요하다.

 

 

페이징 (Paging) 하드웨어 - MMU

우리가 어떤 페이지 번호에 해당하는 프레임 번호를 얻어내기 위해서는 전체 페이지 테이블을 서치하는 것이 아니라 인덱스로 직접 접근할 수 있는 장점이 있다. 하지만 이러한 이유 때문에 페이지 테이블에는 모든 페이지들의 엔트리를 다 가지고 있어야 하는 제약점이 있다. 그래서 페이지 테이블의 크기가 프로그램의 크기와 관계없이 다 일정한 크기이면서 꽤 큰 사이즈를 차지하게 된다. 그렇다면 이 페이지 테이블의 데이터는 어디에 저장이 될까? 이 페이지 테이블이라는 것은 각각의 프로세스마다 하나씩 있어야 되는 것이고 그 크기가 비교적 크기때문에 일반적인 메모리 영역에 페이지 테이블을 저장하게 된다. 이러한 페이징 작업을 하는 주체는 운영체제인 소프트웨어가 아니라 MMU라고 나와있는 하드웨어라는 것이다. CPU에서 나온 논리 주소가 이 MMU를 통해서 자동적으로 물리 주소록 변환되도록 처리하고 있다.

 

페이징의 특징

사용자/ 프로세스의 편의성

연속된 논리 주소 공간을 독립적으로 사용한다 - 주소 변환은 하드웨어와 운영체제에 의해 처리된다.

 

프레임 단위의 비연속적 메모리 할당

동적 메모리 할당에 따른 문제가 없다. -> 외부 단편화가 없다.

 

내부 단편화

페이지 크기보다 작은 메모리를 요청하는 경우에 발생

페이지 크기가 작으면 내부 단편화 감소 - 페이지 테이블 크기 증가

예를들어 페이지 크기가 4KB인데 10KB의 메모리를 필요하는 프로세스는 이 페이지가 2개 하고 2KB할당되는 것이 아니라 3개가 할당되어야지만 10KB메모리를 쓸 수 있다. 그러면 마지막으로 할당된 페이지는 실제로 프로세스가 2KB 만 사용하고 나머지 2KB는 사용하지 않은 메모리가 된다. -> 2KB 내부 단편화 발생

 

프레임 테이블 (frame table)

프로세스마다 각각 다른 페이지 테이블을 가지고 있다. 그래서 운영체제는 실제로 어떤 프레임이 어떤 프로세스의 어떤 메모리에 할당되어있는가라는 정보를 쉽게 찾아내기위해 프레임 테이블을 관리하고 있다. 어떤 프로세스의 어떤 프레임이 사용되고 사용되지 않냐를 빠르게 확인 할 수 있다.

 

페이징와 문맥 교환

페이지 테이블을 재설정하기 위해 문맥 교환 시간이 증가한다. 각 프로세스마다 페이지 테이블이 있고 이 페이지테이블은 메모리에 저장이 돼 있지만 어떤 프로세스를 실행할떄 이 페이지 테이블을 사용하고, 또, 다른 프로세스일땐 다른 페이지 테이블을 사용하면서 메모리에서 다른 페이지 테이블 이미지를 가져와 재설정하게 되어 문맥 교환 시간이 생기게 된다.

 

공유 페이지 (shared page)

각각의 프로세스마다 다른 논리 메모리 공간을 가지고 있지만 그 다른 프로세스들의 특정 페이지가 실제 물리 메모리에는 같은 프레임으로 연결되도록 페이지 테이블 정보를 가지고 있게 된다면 서로 다른 프로세스이지만 동일한 메모리를 사용할 수 있다. 만약 메모리 침범 제약만 관리하게 된다면 프로세스 내에 메모리 공유가 좀 더 간단하게 이루어질 수 있다는 장점이 생기게 된다.

 

반응형

페이지 테이블의 구현

페이지 테이블도 메모리에 저장

기준 레지스터 (Page-Table Base Register, PTBR)에 메모리에 저장된 페이지 테이블의 시작 주소를 저장한다.

문맥 교환 시에 페이지 테이블 교체 비용이 작다. -> PTBR값만 변경하면 된다.

 

메모리 접근 시간 문제

그래서 실질적으로 어떤 메모리에 위치한 변수에 접근하기 위해서는 먼저 이 페이지 테이블이 있는 메모리를 먼저 접근해서 페이지 테이블 데이터를 가지고 온 후 이것을 참조해서 논리 주소를 물리 주소로 변환하는 작업을 거친 후에 실제로 그 메모리에 접근하여 2번 메모리에 접근하는 상황이 발생하게 된다. 이는 페이징 성능상에 중요한 문제가 된다.

 

TLB (Translation Look aside Buffer)

이러한 문제를 해결하기 위한 방법으로 페이지 테이블을 위한 소형의 하드웨어 캐시가 있다

어쨌든 두 번 메모리에 접근해야 하지만 페이지 테이블을 읽는 속도 만큼은 매우 빠르게 한다는 것이 페이지 테이블 캐싱의 원리이다. 그리고 MMU는 이런 페이지 테이블 캐싱을 위해서 컴퓨터 시스템에 있는 캐시 메모리를 그대로 이용하는 것이 아니고 MMU내에 TLB라고 하는 페이지 테이블만 전용으로 캐싱하는 별도의 캐시 메모리를 두게 된다.

 

특징

접근 속도가 매우 빠른 연관 메모리 (associative memory)

TLB 내의 각 항목(entry)은 키(key)와 값(value)로 구성되며 key는 페이지 번호, value는 페이지 번호에 해당하는 프레임 번호이다.

요청된 페이지 번호로 모든 항목을 동시에 비교 가능하며 비싼 메모리로써 보통 64 ~ 1024 항목만이 저장된다.

메모리 참조 시간은 주소 변환을 하지 않는 경우보다 10% 이하의 시간만 더 소요된다.

 

TLB로 접근하는 것은 매우 빠르게 접근할 수 있는 것이고 page table은 메모리 참조시간과 동일하다고 할 수 있다. 그렇지만 TLB가 있다고 해서 페이지 테이블을 완전히 사용하지 않을 수는 없다. 왜냐하면 TLB는 페이지 테이블 전체 중에 일부만 담고있는 것이기 때문에 TLB에 포함되어 있지 않는 페이지 번호인 경우에는 어쩔 수 없이 페이지테이블에 접근해서 그 프레임 번호 값을 읽어내야 한다. 따라서 전체적으로 MMU 하드웨어가 주소변환을 하는 과정을 살펴보자면 CPU가 메모리를 참조하기 위해서 그 데이터의 논리 주소를 꺼내게 될 것이다. 그러면 이 논리주소중에서 페이지 번호에 해당하는 부분을 가지고서 페이지 테이블 참조를 할 텐데 이 때는 일단 TLB를 먼저 참조하게 된다. 그런데 TLB는 페이지테이블의 일부만 갖고 있기 때문에 인덱스를 바로 참조하는 것이 아니고 내가 가지고 있는 페이지 번호가 TLB안에 있는지를 검색을 해야한다. 그리고 검색한 결과 해당 페이지번호가 있다면 프레임 번호를 얻어내어 물리 주소를 형성하게 되는 것이다. 이렇게 되면 빠른 속도로 프레임 번호를 얻을 수 있다.(TLB hit)  하지만 원하는 페이지 번호가 없다면 이는 TLB miss 라고 하는 것이고 이렇게 되면 어쩔 수 없이 TLB 참조 후에 메모리 안에 저장되어 있던page table도 참조를 해야한다. 그래서 이렇게 TLB miss가 나게되면 TLB가 없을 때보다 더 긴 시간이 걸리게 된다. 따라서 이 시스템이 원할하게 잘 동작 하려면 TLB에서 내가 원하는 페이지를 찾을 확률이 매우 높아야만 한다.

 

페이지 테이블의 구조

실제 컴퓨터 시스템에서의 페이지 테이블

페이지 테이블의 크기가 매우 크다.

실제 컴퓨터 시스템의 논리 주소 공간: 2^32 혹은 2^64

페이지 크기: 4KB (2^12)

페이지 테이블 항목(entry)크기: 4bytes

페이지 테이블의 크기: 4MB (4*2^(32-12))

 

이렇게 페이지 테이블의 크기가 꽤 크기 때문에 페이지 테이블을 연속된 메모리 공간에 배치하기가 어렵다. 앞서 연속 메모리 할당에서 나왔던 문제처럼 비효율적인 메모리 공간 배치가 될 수 있다. 그래서 이렇게 큰 페이지 테이블을 메모리 상에 어떻게 저장할지에 대해 구현하는 것도 꽤 중요한 이슈가 된다.

크기가 큰 페이지 테이블의 처리

계층적 페이징 (Hierarchical Paging)

해시 페이지 테이블 (Hashed Page Table)

역 페이지 테이블 (Inverted Page Table)

 

계층적 페이징 (Hierarchical Paging)

2단계 페이지 테이블 기법

프로세스마다 4MB의 페이지테이블을 저장하고 여러 프로세스들에 대한 페이지테이블 저장공간을 연속적으로 배치하게 된다면 꽤 많은 공간을 차지하게 된다. 그래서 계층적 페이징은 페이지 테이블을 이루는 큰 메모리 공간도 페이지 단위로 나누어서 실제 메모리에 연속되지 않게 배치한다라는 것을 의미한다. 이렇게 하기 위해서는 페이지 테이블을 구성하는 각각의 페이지들에 대해서 시작 위치를 알고 있어야 페이지 번호로 바로 인덱스에서 원하는 값을 찾아낼 수가 있게 된다. 그래서 이러한 방식으로 페이지 테이블을 운영하기 위해서는 별도의 페이지 테이블의 페이지들을 찾기위한 추가의 페이지 테이블이 필요하게 된다. (이 4MB마저도 쪼개서 관리한다는 뜻 )

 

2단계 페이징에서 주소 변환

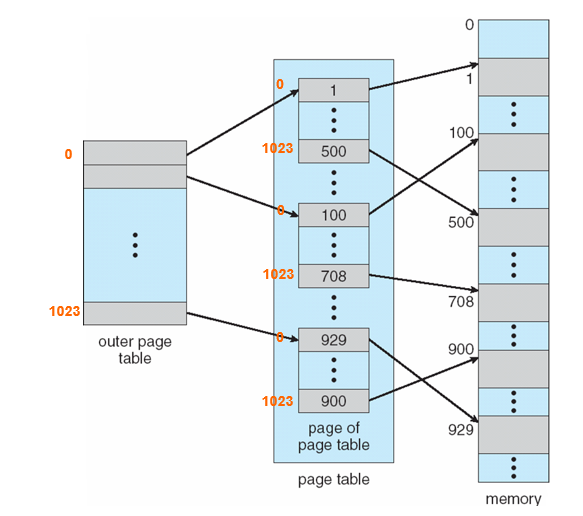
즉 위 예시와 같이 32비트 논리 주소 공간의 2단계 페이징 주소 구조는 다음과 같다

20비트의 페이지 번호를 갖고 있는데 10비트는 외부 페이지 테이블의 인덱스 (페이지 번호)이며 나머지 10비트는 페이지 테이블을 위한 페이지의 오프셋이라고 할 수 있다.

앞에서 페이지테이블의 크기가 4MB가 나왔는데 여기서 페이지의 개수는 2^20개 였다. 2단계 페이징에서는 이것을 더 쪼개어 4KB짜리 페이지 테이블을 2^10 개 로 나누어 페이지 테이블로 구성을 할 수 있다는 뜻이다. 또한 32비트 논리 주소 공간이 아닌 64비트 논리 주소 공간을 가진 시스템에서는 페이지테이블 항목 (entry) 크기가 64bit 즉 8byte가 되면서 3단계 이상의 페이징을 사용하고 있다. 이렇게 계층적 페이지 테이블은 주소 변환 시간이 길어져서 사실상 비현실적인 구현이다. 그래서 유효한 페이지들만 테이블에 포함하는 hashing 기법이 생겨났다.

 

해시 페이지 테이블 (Hashed Page Table)

논리 주소의 페이지 번호를 해시 값으로 사용

32비트 이상의 논리 주소 공간을 위한 페이지 테이블 구성방법

같은 위치에 해당되는 해시 페이지 테이블의 항목은 연결 리스트 구성 - 페이지 번호, 프레임 번호, 다음 원소 포인터

 

역 페이지 테이블 (Inverted Page Table)

 

물리 메모리의 프레임 번호로 인덱스되는 테이블

원래 페이지 테이블에서는 프로세스의 논리 주소를 인덱스로 하고 어떤 해싱을 해서 실제 메모리의 프레임 주소로 바꿔준다. 이때 논리 주소 공간의 관점에서 보면 실제 프로세스가 사용하지 않는 것들에 대해서도 페이지 테이블 엔트리를 유지하기 때문에 이 공간의 낭비가 생기게 된다. 하지만 반대로 메모리(RAM)의 관점에서 보면 RAM의 모든 위치들은 어떤 순간 어느 한 프로세스에 할당된 것이다. 그래서 논리 주소를 물리 주소로 바꿔주는 방식의 테이블이 아닌 반대로 물리 주소를 논리 주소로 바꿔주는 테이블을 만드는 것이 바로 역페이지 테이블이다.

 

주소 변환

논리주소: <프로세스 ID, 페이지 번호, 오프셋>

프로세스 ID와 페이지 번호로 페이지 테이블을 검색 (search)

발견된 항목의 인덱스가 프레임 번호

 

역 페이지 테이블의 특징

작은 메모리 공간 필요하고 주소 변환 시간이 길어진다 (검색비용) -> 해시 테이블의 사용을 요구한다. 또한 메모리 공유가 어렵다.

 

 

세그멘테이션 (Segmentation)

프로세스가 필요하는 전체 논리에 메모리 공간을 한 덩어리로 메모리에 연속적으로 할당하는 것이 아니라 여러개의 작은 단위로 쪼갠 다음에 메모리를 할당한다라는 방법이 된다. 이것이 페이징하고 다른 점은 페이징에서는 분할하는 단위가 고정된 크기의 페이지 였다면 세그멘테이션에서는 프로그램의 논리적인 단위에 따라 프로세스의 메모리 공간을 구분한다는 것이다. 논리적 단위로는 method, procedure, function, object, variables, stack 등 함수단위로 나눌 수 있고 C컴파일러 관점에서는 코드, 전역 변수, 힙, 스택, 표준 C 라이브러리 단위로 구분지어 나눌 수 있다. 세그먼트의 논리 주소는 세그먼트의 이름(번호)와 오프셋으로 나뉜다.

 

세그먼트 테이블 (segment table)

세그먼트 테이블에서는 각각의 세그멘트가 차지하는 크기가 서로 다르기 때문에 각 세그멘트가 실제 메모리의 어떤 위치에 저장되어 있느냐라는 정보와 함께 끝 주소 즉 크기까지 같이 포함하고 있는 정보를 가지고 있는 것이 세그멘테이션 세그먼트 테이블이라고 할 수 있다.

 

세그멘테이션 하드웨어 

 

논리 주소는 세그먼트 번호와 세그먼트 안에 오프셋으로 구성되어 있다. 그리고 세그먼트 테이블에서 시작 주소와 그 세그먼트 테이블의 끝 주소를 읽어내고 끝 주소하고 내부에서 오프셋 위치를 비교를 하게 된다. 그래서 오프셋 위치는 당연히 끝 주소보다 더 작아야 된다. 만약에 더 크다면 잘못된 세그먼트를 침범한다고 할 수 있다.